GAPCOIN

Home

Mining

Downloads

Road Map

Prime Gaps

What is Gapcoin?

Gapcoin is a new prime number based p2p cryptocurrency, which tries to eliminate the sticking points of other scientific currencies like Primecoin or Riecoin.
It's a fork of Satoshi Nakamotos Bitcoin, a decentralized payment system which is independent of banks, governments and other centralized regulators.
With Gapcoin, you will be able to anonymously send money around the globe in no time.

The big improvement in comparison to Bitcoin is that instead of burning electricity for its own sake, Gapcoins Proof of Work function actually does useful work by searching for large prime gaps.

 

Specifications:

• PoW: custom, prime gaps
• Block target time 2.5 minutes
• Block reward proportional to the current difficulty
• Block reward halving every 420000 (about 2 years)
• Cap: about 10 - 30 million GAP
• Difficulty adjusts every block and increases logarithmically (it will probably take years to get to 50)

 

Fair launch:

• Gapcoin was not designed to enrich the early adopters or the coin creators! Unlike Primecoin, the more people mine Gapcoin, the more coins per block will be produced. (Coin supply will increase logarithmically with the difficulty, this means it will grow in the beginning, but later, it won't change much.)
• There won't be any premine!
• To avoid instamine, the reward of the first 1152 blocks (about 48 hours) will increase quadratically to its absolute value: the current difficulty. Block reward will be 1/1152^2 * blockheight^2 * difficulty for the first 1152 blocks.
• Source code will be available before launch (excluding the PoW function), so everyone can setup their own environment, compile the software, and check if everything works.
• Windows and Linux binaries will be distributed in an encrypted container before launch, the password will be revealed at launch.

 

How is Proof of Work actually designed?

A PoW algorithm has to fit two specifications:

• It must be cryptographically secure (a PoW must not be reusable)
• It must be hard to calculate, but easy to verify

Verifying a prime gap is easy, you only have to check every number between the start and the end to be composite.

Calculating is harder, much harder!
Large prime gaps occur a lot lesser than smaller ones. According to E. Westzynthius, in e^n prime gaps there will be one gap that is n times greater than the average prime gap.

So the difficulty will simply be the length of the prime gap?

Not exactly. The average length of a prime gap with the starting prime p, is log(p), which means that the average prime gap size increases with lager primes.
Then, instead of the pure length, we use the merit of the prime gap, which is the ratio of the gap's size to the average gap size.

Let p be the prime starting a prime gap, then m = gapsize/log(p) will be the merit of this prime gap.

Also a pseudo random number is calculated from p to provide finer difficulty adjustment.

Let rand(p) be a pseudo random function with 0 < rand(p) < 1
Then, for a prime gap starting at prime p with size s, the difficulty will be s/log(p) + 2/log(p) * rand(p), where 2/log(p) is the average distance between a gap of size s and s + 2 (the next greater gap) in the proximity of p.

When it actually comes to mining, there are two additional fields added to the Blockheader, named “shift” and “adder”.
We will calculate the prime p as sha256(Blockheader) * 2^shift + adder.
As an additional criterion the adder has to be smaller than 2^shift to avoid that the PoW could be reused.

 

Could we break any world records?

We already broke 544 records of first known occurrence prime gaps.

Also, if the difficulty reaches 35.4245, every block will be a new world record: Top 20 Prime Gaps

But how are prime gaps useful?

Prime numbers are interesting for lots of mathematicians around the globe, and they're also important to every day cryptography (see RSA).

Researches about prime gaps could not only lead to new breakthroughs in the bounded gap, it may also help proving the Twin Prime Conjecture and maybe even the millennium problem, the Riemann hypothesis. Who knows?

 

Last but not least, what does the logo have to do with prime gaps?

Well, the “G” was already taken by Goldcoin, so that was no possibility.
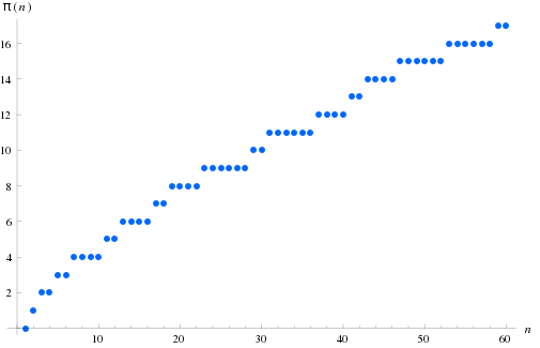
But the formula π(x) is known as the prime-counting function, which graph shows the prime gap distribution as well. That's why the “π” fits the logo perfectly. (image Wikipedia)

Contact

        info@gapcoin.org

Mailing list

unsubscribe

Windows Wallet

       Windows 32 and 64 bit binaries

Linux Wallet

       Linux 32 and 64 bit binaries

Source code

       github

Exchanges

       Cryptopia

       Nova Exchange

Block Explorer

       cryptoID

Community

       Bitcointalk

       Reddit

       Twitter

 

Donations

    [GAP] GapCoinh1amMiRq56WunADY4yztmNBMaYr

    [BTC] 1Dv8e3WfhuiBhgNJo6RbvU1nXzF7goifHS

    [LTC] LQRFrMsiFQAuC8rnns9wt9cE2VdqhX9gSc

    [XPM] AKS71YssSJTP7J1CFDzysr5ijnyyvioekg

    [RIC] RYE7GyMYu2VZs9Y2dkXTuVf4TtZ8YTExJK